400年ぶりの発見!?対称性多面体とは
2014年2月、400年ぶりに新種の
『対称性多面体(たいしょうせいためんたい)』
構造が発見されました。
4つ以上の平面に囲まれた立体を『多面体』と呼びますが
中でもすべての面が『合同の正多角形(形と大きさが同じであること)』
で構成される『正多面体』は最も美しい対称性を持つ立体で
わずか5種類しかないことが知られています。
しかし、条件を少し緩くすることで
正多面体の亜種とも言える
対称性を持つ多面体が考え出されてきました。
そして、400年ぶりにその新種が
アメリカの数学者によって考案されたのです。
ここでは、『対称性』と『多面体』の
それぞれの用語についてご紹介してから
今回のニュースについて詳しく見ていきたいと思います。
『対象性』とは?
『対称性』とは『シンメトリー』とも呼ばれ回転などの変換をしても変わらない性質のことを指します。
ここでは、算数や数学の授業でも習う『線対称』、
『点対称』、『面対称』について詳しく見ていきたいと思います。
線対称とは、1本の直線を折り目として
ある図形が完全に重なりあうことを言います。
また、この直線を『対称軸』と呼びます。
点対称とは、どこか1点を基準として
180度回転したときに図形が完全に重なり合うことを言います。
面対称とは1つの平面を平面鏡として
ある図形がその平面鏡に映した物体と像のような関係にあることを言います。
図形の対称性についてお伝えしましたが
式の文字を入れ替えても元の式と変わらない式を『対称式』と呼ぶなど
その言葉が指し示すものは広範囲に渡っています。
簡単に言えば
対称とは『どこから見ても同じ』
といったイメージです。
正多面体は5種類だが、条件を緩和すれば新種も
さて、続いてはもうひとつの用語である『多面体』についてご紹介します。
多面体とは、複数(4つ以上)の平面に囲まれた
立体のことを言います。
折り紙をイメージするとわかりやすいですが
平面が3つ以下では立体を作ることができません。
また、多面体の特徴はすべての面の境界が直線であることが挙げられ
曲面を持つものは含まれません。
多面体には多くの種類があり
『角柱』や『角錐(かくすい)』などがありますが
ここでご紹介したいのは『正多面体』です。
正多面体とは『プラトンの立体』とも呼ばれるもので
すべての面が同じ正多角形で構成されてあり
かつすべての頂点において接する面の数が等しい
凸多面体(凹んでいない多面体のこと)を指します。
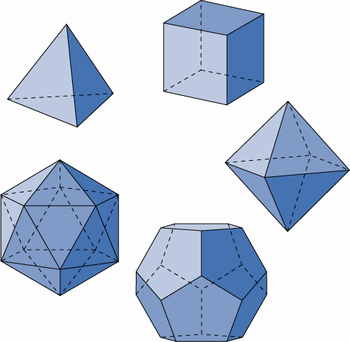
正多面体には
正四面体
正六面体
正八面体
正十二面体
正二十面体
の5種類があります。
しかし、『すべての面が同じ正多角形で構成される』
という条件を緩和することにより
『半正多面体(アルキメデスの立体)』が考案されました。
サッカーボールの形として知られる
『切頂二十面体』が特に有名です。
さらに、正多面体は『凸多面体であること』を条件としていますが
これを緩和することにより
『星型正多面体(ケプラー・ポアンソの立体)』2種類を
ドイツの数学者ヨハネス・ケプラーが発見しました。
折り紙を組み合わせて作った経験がある方も多いと思います。

そして、さらに2種類の星型正多面体が発見されましたが
それ以降は発見されていませんでした。
曲面を認めれば、新しい対称性多面体が作れる
さて、前置きが長くなりましたがここからは400年ぶりに発見された対象性多面体のお話です。
カリフォルニア大学のスタン・シェイン博士は目の網膜の研究をする過程で
『クラスリン』と呼ばれるたんぱく質の構造に興味を持ちました。
そして、その立体構造を数学的に解析するうちに
20世紀の数学者マイケル・ゴールドバーグ博士の考案した多面体を見つけます。
この立体は、構成する面が平面ではないことから
厳密には多面体としては考えられていません。
しかし、この立体にヒントを得たシェイン博士は
多面体構造の前提条件『面が平面である』という部分を緩和して
完全な平面ではない『ねじれた面構造』を許すことで
新たに対象性を持つ『対称性・準多面体』とも言うべき
立体を考案することに成功しました。
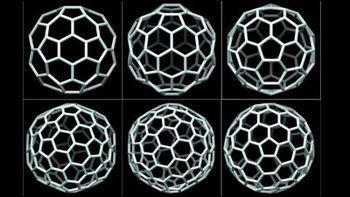
具体的には、立体を構成する六角形の面は
ねじれた構造をしているものの美しい対称性を描いています。
また、ねじれ具合を調整して面の数を増やすことで
このような立体は無限に作り出せる可能性があるとのことです。
今回の発見は、多面体の前提条件から外れた立体であるため
新しい対称性多面体であると呼べるかどうかはまだ分かりません。
しかし、この立体構造は特定のインフルエンザウイルスが持つ構造ではないか
と見られており、ウイルスの構造を把握して治療技術を確立するのに
応用できるのではないかと期待されています。
